inequalities problem solving questions

Examples of Inequalities Word Problems With Solutions

Inequalities are a powerful tool that is taught in high school mathematics that allows us to solve a variety of real-life situations where a range of multiple solutions are possible.

Inequalities help us model scenarios with constraints such as budgeting, scheduling, or meeting minimum requirements, while guiding us toward finding the most practical range of solutions.

My goal is to walk you through a few key tips and examples to master solving linear inequality word problems with solutions that show you each step!

What Are Inequality Word Problems?

An inequality is a mathematical statement that shows the relationship between two expressions using symbols.

Inequality statements involve one of the following symbols:

• < (less than)
• > (greater than)
• ≤ (less than or equal to)
• ≥ (greater than or equal to)

Unlike equations, inequalities provide a range of possible values that satisfy specific conditions. Inequalities word problems require us to find the set of solutions that make an inequality statement true.

In real world problems, linear inequalities are commonly used to represent scenarios with limits, such as “at least 5” or “no more than 10.”

We can translate these statements into mathematical models by identifying key words and assigning appropriate variable names to unknowns.

My Top Tips for Solving Inequality Word Problems

When solving an inequality algebraically, we apply the same algebraic equation solving strategies that you have learned!

Before diving into some examples of inequalities word problems, I want to share some strategies for solving these problems effectively. These tips are similar to my strategies for solving math word problems .

• Choose Clear Variable Names : Use names that represent the context of the problem. For example, we might choose to let \(x\) represent the quantity given in the problem. Depending on the scenario, this could represent the number of items, an average speed, etc.
• Identify the Key Words Used : Be on the lookout for phrases like “at least,” “no more than,” and “maximum”. These phrases give you specific information about how to set up your inequality. I always recommend underlining these in the problem so that you can clearly see all of the key words while formulating a plan.
• Translate the Word Problem to a Mathematical Model : Use the appropriate symbol that matches the key words you underlined. Write an inequality that captures the relationships in the problem.
• Check Your Work : After solving the inequality word problem, substitute a few test values into the original problem to ensure they satisfy all conditions.

Let’s take a look at how these tips for solving inequality word problems can be used to solve some problems!

Examples of Inequalities Word Problems

Let’s dig into some real-life situation examples of inequalities word problems. I have also provided a solution answer key for each of the problems with detailed explanations of each step!

Example 1: Budgeting for a Scavenger Hunt

A group is organizing a scavenger hunt and must spend at least $50 on prizes to qualify for a group discount. Each prize costs $8. How many prizes do they need to buy to meet this minimum spending requirement?

We can begin by letting \(x\) represent the number of prizes. We can write a statement that uses the  greater than or equal to  symbol since we know that the group needs to spend  a minimum of  $50 (or  at least  $50).

Since each prize costs $8, we know that we will be multiplying 8 by our variable of \(x\). This results in the following inequality statement: 

\[8x \geq 50\]

We can solve by dividing both sides of the inequality by 8:

\[\begin{split} x &\geq \frac{50}{8} \\ \\ x & \geq 6.25 \end{split}\]

Since we know that we can’t have fractional prizes, we must round up to the next whole number to ensure the spending meets the minimum requirement.

Therefore, the group must buy at least 7 prizes.

Example 2: Average Speed Problem

A student drives to school and wants to arrive on time for an 8:00 AM class. If the school is 20 miles away and they leave at 7:30 AM, what minimum speed must they maintain to avoid being late?

Let’s start by letting \(s\) represent the speed in miles per hour.

We know that there is a relationship between distance, average speed, and time. This relationship is \(time=\frac{distance}{speed}\). We can use this relationship to create an inequality statement.

Since we are told that the student must arrive within a half hour, we know that we will be using  a less than or equal  to symbol in our statement. Substituting our distance and time into our equation results in:

\[\begin{split}  \frac{distance}{speed} &\leq 0.5 \\ \\ \frac{20}{s} &\leq 0.5 \\ \\ \frac{20}{0.5} &\leq s \\ \\ 40 &\leq s \end{split}\]

We can rewrite this solution as \(s \geq 40\) to show that speed must be greater than or equal to 40 miles per hour.

Therefore, we can conclude that the student must drive at least 40 miles per hour to arrive on time!

Example 3: Determining the Number of Girls in a Club

In a school club, there are at least twice as many boys as girls. If there are 12 boys, determine the number of girls that there could be in the club.

Let’s begin by letting the variable \(g\) represent the number of girls. We know that the number of boys is twice the number of girls. We represent this as \(2g\) in our inequality statement. In total, this amount has to be less than or equal to 12.

We set up our inequality statement as:

\[\begin{split}  2g &\leq 12 \\ \\ g &\leq \frac{12}{2}  \\ \\ g &\leq 6 \end{split}\]

Therefore, we can conclude that there can be up to 6 girls in the club.

Looking for some more practice? Check out my collection of linear inequalities worksheets ! Then, use this inequalities word problem worksheet to solidify your understanding!

Did you find these examples of inequalities word problems with solutions helpful? Share this post and subscribe to Math By The Pixel on YouTube for more helpful mathematics content!

RECOMMENDED FOR YOU

How to Solve Population Growth Math Problems (With Examples)

Quadratic Formula Word Problems Answer Key and Lesson

Solving Inequality Word Questions

(You might like to read Introduction to Inequalities and Solving Inequalities first.)

In Algebra we have "inequality" questions like:

Sam and Alex play in the same soccer team. Last Saturday Alex scored 3 more goals than Sam, but together they scored less than 9 goals. What are the possible number of goals Alex scored?

How do we solve them?

The trick is to break the solution into two parts:

Turn the English into Algebra.

Then use Algebra to solve.

Turning English into Algebra

To turn the English into Algebra it helps to:

• Read the whole thing first
• Do a sketch if needed
• Assign letters for the values
• Find or work out formulas

We should also write down what is actually being asked for , so we know where we are going and when we have arrived!

The best way to learn this is by example, so let's try our first example:

Assign Letters:

• the number of goals Alex scored: A
• the number of goals Sam scored: S

We know that Alex scored 3 more goals than Sam did, so: A = S + 3

And we know that together they scored less than 9 goals: S + A < 9

We are being asked for how many goals Alex might have scored: A

Sam scored less than 3 goals, which means that Sam could have scored 0, 1 or 2 goals.

Alex scored 3 more goals than Sam did, so Alex could have scored 3, 4, or 5 goals .

• When S = 0, then A = 3 and S + A = 3, and 3 < 9 is correct
• When S = 1, then A = 4 and S + A = 5, and 5 < 9 is correct
• When S = 2, then A = 5 and S + A = 7, and 7 < 9 is correct
• (But when S = 3, then A = 6 and S + A = 9, and 9 < 9 is incorrect)

Lots More Examples!

Example: Of 8 pups, there are more girls than boys. How many girl pups could there be?

• the number of girls: g
• the number of boys: b

We know that there are 8 pups, so: g + b = 8, which can be rearranged to

We also know there are more girls than boys, so:

We are being asked for the number of girl pups: g

So there could be 5, 6, 7 or 8 girl pups.

Could there be 8 girl pups? Then there would be no boys at all, and the question isn't clear on that point (sometimes questions are like that).

• When g = 8, then b = 0 and g > b is correct (but is b = 0 allowed?)
• When g = 7, then b = 1 and g > b is correct
• When g = 6, then b = 2 and g > b is correct
• When g = 5, then b = 3 and g > b is correct
• (But if g = 4, then b = 4 and g > b is incorrect)

A speedy example:

Example: Joe enters a race where he has to cycle and run. He cycles a distance of 25 km, and then runs for 20 km. His average running speed is half of his average cycling speed. Joe completes the race in less than 2½ hours, what can we say about his average speeds?

• Average running speed: s
• So average cycling speed: 2s
• Speed = Distance Time
• Which can be rearranged to: Time = Distance Speed

We are being asked for his average speeds: s and 2s

The race is divided into two parts:

• Distance = 25 km
• Average speed = 2s km/h
• So Time = Distance Average Speed = 25 2s hours
• Distance = 20 km
• Average speed = s km/h
• So Time = Distance Average Speed = 20 s hours

Joe completes the race in less than 2½ hours

• The total time < 2½
• 25 2s + 20 s < 2½

So his average speed running is greater than 13 km/h and his average speed cycling is greater than 26 km/h

In this example we get to use two inequalities at once:

Example: The velocity v m/s of a ball thrown directly up in the air is given by v = 20 − 10t , where t is the time in seconds. At what times will the velocity be between 10 m/s and 15 m/s?

• velocity in m/s: v
• the time in seconds: t
• v = 20 − 10t

We are being asked for the time t when v is between 5 and 15 m/s:

So the velocity is between 10 m/s and 15 m/s between 0.5 and 1 second after.

And a reasonably hard example to finish with:

Example: A rectangular room fits at least 7 tables that each have 1 square meter of surface area. The perimeter of the room is 16 m. What could the width and length of the room be?

Make a sketch: we don't know the size of the tables, only their area, they may fit perfectly or not!

• the length of the room: L
• the width of the room: W

The formula for the perimeter is 2(W + L) , and we know it is 16 m

• 2(W + L) = 16
• L = 8 − W

We also know the area of a rectangle is the width times the length: Area = W × L

And the area must be greater than or equal to 7:

• W × L ≥ 7

We are being asked for the possible values of W and L

Let's solve:

So the width must be between 1 m and 7 m (inclusive) and the length is 8−width .

• Say W = 1, then L = 8−1 = 7, and A = 1 x 7 = 7 m 2 (fits exactly 7 tables)
• Say W = 0.9 (less than 1), then L = 7.1, and A = 0.9 x 7.1 = 6.39 m 2 (7 won't fit)
• Say W = 1.1 (just above 1), then L = 6.9, and A = 1.1 x 6.9 = 7.59 m 2 (7 fit easily)
• Likewise for W around 7 m

• Testimonial
• Web Stories

Learning Home

Not Now! Will rate later

Inequalities : Practice Problems

• Rational & Modulus Inequalities: Theory & Concepts
• Inequalities: Solved Examples
• Higher order inequalities: Theory & Concepts
• Inequalities: Practice Problems

Most Popular Articles - PS

Time and Work Concepts

Time and Work Formula and Solved Problems

Time and Work Problems (Easy)

Time and Work Problems (Difficult)

Problems on Ages Practice Problems : Level 02

Chain Rule : Theory & Concepts

Chain Rule Solved Examples

Chain Rule Practice Problems: Level 01

Chain Rule Practice Problems : Level 02

Problems on Numbers System : Level 02

Download our app.

• Learn on-the-go
• Unlimited Prep Resources
• Better Learning Experience
• Personalized Guidance

Get More Out of Your Exam Preparation - Try Our App!

• Number System and Arithmetic
• Probability
• Mensuration
• Trigonometry
• Mathematics

Linear Inequalities Practice Questions

Linear inequalities are fundamental concepts in algebra that help us understand and solve a wide range of real-world problems. These inequalities express the relationship between two expressions using inequality symbols like <, ≤, >, and ≥. Learning to solve linear inequalities involves understanding how to manipulate these expressions to isolate the variable and determine the range of possible solutions.

In this article, we will explore various practice questions on linear inequalities to enhance your understanding and problem-solving skills. We will cover single-variable inequalities, systems of linear inequalities, and graphical representations of these solutions. Each section includes step-by-step explanations to help you grasp the methods used in solving different types of inequalities.

What are Linear Inequalities?

Linear inequalities are mathematical expressions involving linear functions that use inequality symbols (such as <, ≤, >, or ≥) instead of an equality sign. These inequalities describe a relationship where one side of the expression is not strictly equal to the other but is either less than, greater than, or equal to (depending on the inequality used).

Examples of Linear Inequalities

• One-Step Linear Inequality: x − 7 > 10
• Two-Step Linear Inequality: 5x + 4 ≤ 19
• Linear Inequality with Negative Coefficient: 20 − 3x < 8
• Compound Inequality: −3 < 4x + 1 ≤ 17

Solved Problems on Linear Inequalities

Problem 1: Solve the inequality: x - 5 ≤ 3.

Given: x - 5 ≤ 3 Add 5 to both sides to isolate x: x - 5 + 5 ≤ 3 + 5 ⇒ x ≤ 8 Thus, x ∈ (-∞, 8]

Problem 2: Solve the inequality: 4x - 7 > 9

Given: 4x - 7 > 9 Add 7 to both sides: 4x - 7 + 7 > 9 + 7 ⇒ 4x > 16 Divide both sides by 4: x > 4 Thus, x ∈ (4, ∞)

Problem 3: Solve the inequality: -2x + 6 ≥ 8

Given: -2x + 6 ≥ 8 Subtract 6 from both sides: -2x + 6 - 6 ≥ 8 - 6 ⇒ -2x ≥ 2 Divide both sides by -2, reversing the inequality sign: x ≤ -1 Thus, x ∈ (-∞, -1]

Problem 4: Solve the inequality: -2 < 3x - 5 ≤ 7

Given: -2 < 3x - 5 ≤ 7 Add 5 to all parts: -2 + 5 < 3x - 5 + 5 ≤ 7 + 5 ⇒ 3 < 3x ≤ 12 Divide all parts by 3: 1 < x ≤ 4 Thus, x ∈ (1, 4]

Problem 6: Solve the inequality: 5(2x - 1) ≤ 3(3x + 4)

Given: 5(2x - 1) ≤ 3(3x + 4) Distribute the constants: 10x - 5 ≤ 9x + 12 Subtract 9x from both sides: 10x - 9x - 5 ≤ 12 ⇒ x - 5 ≤ 12 Add 5 to both sides: x ≤ 17 Thus, x ∈ (-∞, 17]

Problem 7: Solve the inequality: 4x + 7 > 2x - 5

Given: 4x + 7 > 2x - 5 Subtract 2x from both sides: 4x - 2x + 7 > 2x - 2x - 5 ⇒ 2x + 7 > -5 Subtract 7 from both sides: 2x > -12 Divide both sides by 2: x > -6 Thus, x ∈ (-6, ∞)

Problem 8: Solve the inequality: \frac{2x - 3}{4} \leq 1 .

Given: \frac{2x - 3}{4} ≤ 1 Multiply both sides by 4 to eliminate the fraction: 4 \cdot \frac{2x - 3}{4} ≤ 1 \cdot 4 ⇒ 2x - 3 ≤ 4 Add 3 to both sides: 2x - 3 + 3 ≤ 4 + 3 ⇒ 2x ≤ 7 Divide both sides by 2: x ≤ 7/2 ⇒ x ≤ 3.5 Thus, x ∈ (-∞, 3.5]

Problem 10: Solve the inequality: 3 < 2(x + 1) ≤ 7

Given: 3 < 2(x + 1) ≤ 7 Divide the compound inequality into two parts and solve each separately. Solve 3 < 2(x + 1): Divide by 2: 3/2 < x + 1 Subtract 1 from both sides: 3/2 - 1 < x ⇒ 1/2 < x Solve 2(x + 1) ≤ 7: Divide by 2: x + 1 ≤ 7/2 Subtract 1 from both sides: x ≤ 5/2 Combine the solutions: 1/2 < x ≤ 5/2 Thus, x ∈ (1/2, 5/2]

Practice Problems on Linear Inequalities

Problem 1: Solve the inequality:

3x - 4 ≤ 2x + 5

Problem 2: Solve the compound inequality:

-2 ≤ 4 - 3x < 10

Problem 3: Solve the inequality and graph the solution:

(2x + 3)/5 > 1

Problem 4: Solve the system of inequalities:

• x - y < 2

Problem 5: Solve the inequality:

5 - 2(x - 3) ≥ 3(x + 4) - 7

Problem 6: Solve the compound inequality:

-1 < 2x + 1 ≤ 5

Problem 7: Solve the inequality:

4(2x - 1) < 3(x + 6)

Problem 8: Solve the inequality:

7 - 3(2x + 1) ≥ 2(3 - x) + 1

Problem 9: Solve the inequality and represent the solution on a number line:

\frac{3x - 2}{4} ≤ \frac{x + 5}{2}

• Inequalities
• Inequalities Practice Questions with Solution
• Linear Inequalities
• Graphical Solution of Linear Inequalities in Two Variables
• Solving Linear Inequalities Word Problems
• Quadratic Inequalities

FAQs: Linear Inequalities

What are linear inequalities.

Linear inequalities are mathematical expressions that show the relationship between two expressions using inequality symbols (<, ≤, >, ≥).

What is a compound inequality?

A compound inequality involves two or more inequalities joined by "and" or "or". An "and" compound inequality means both conditions must be true simultaneously, while an "or" compound inequality means at least one of the conditions must be true.

How do you represent the solution of a linear inequality?

The solution of a linear inequality can be represented using interval notation, a number line, or a shaded region on a graph.

What is the difference between a linear equation and a linear inequality?

A linear equation uses an equal sign (=) to show that two expressions are equal, while a linear inequality uses inequality symbols (<, ≤, >, ≥) to show that one expression is less than, greater than, or equal to the other.

Can linear inequalities have more than one variable?

Yes, linear inequalities can have more than one variable. For example, 2x + 3y ≤ 6 is a linear inequality with two variables.

What does it mean to reverse the inequality sign?

When you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality sign to maintain the correct relationship.

Can a system of linear inequalities have no solution?

Yes, a system of linear inequalities can have no solution if there is no region that satisfies all the inequalities simultaneously.

Similar Reads

• Linear Inequalities Practice Questions Linear inequalities are fundamental concepts in algebra that help us understand and solve a wide range of real-world problems. These inequalities express the relationship between two expressions using inequality symbols like <, ≤, >, and ≥. Learning to solve linear inequalities involves unders 6 min read
• Quadratic Inequalities Practice Questions Quadratic inequalities are an essential part of algebra, involving expressions where a quadratic polynomial is set to be greater than or less than a certain value. Practicing quadratic inequalities helps in understanding the range of values that satisfy these inequalities, which is crucial for solvi 10 min read
• One-Step Equations Practice Questions Basic algebraic equations, known as one-step equations. They can be solved in one step by applying addition, subtraction, multiplication, or division. The objective is to carry out the inverse operation on both sides of the equation in order to isolate the variable. For instance, to find x in an equ 3 min read
• Inequalities Practice Questions with Solution Inequalities Practice Questions with Solution: Inequalities are fundamental in mathematics and are used extensively in various branches such as algebra, calculus, optimization and more. They describe relationships between variables and constants and are essential in solving problems involving ranges 6 min read
• Practice Questions on Quadratic Equations Quadratic equations are everyday concepts with real-life applications. Understanding them is essential for solving aptitude and reasoning questions. This article offers a variety of easy-to-understand quadratic equations questions. Whether you’re a student or want to enhance your aptitude and reason 7 min read
• Two-Step Equations Practice Questions Two-step equations are algebraic equations that require two inverse operations to isolate the variable and calculate its value. Typically, these equations involve a sequence of operations, such as addition or subtraction followed by multiplication or division. For example, to solve 2x+3=11, subtract 4 min read
• Solving Linear Inequalities Word Problems We are well versed with equations in multiple variables. Linear Equations represent a point in a single dimension, a line in a two-dimensional, and a plane in a three-dimensional world. Solutions to linear inequalities represent a region of the Cartesian plane. It becomes essential for us to know ho 11 min read
• Linear Inequalities Linear Inequalities in Algebra are defined as the mathematical statements that are formed by combining linear algebraic expressions with inequalities. A linear algebraic expression in an expression with degree one. Linear inequalities can be easily represented using various methods that are discusse 15+ min read
• Algebraic Expressions Practice Questions Algebraic expressions are fundamental components of algebra that represent quantities and relationships using variables, constants, and operations. They form the basis for solving equations and understanding mathematical relationships. In this article, we will learn what algebraic expressions are an 5 min read
• Algebra Practice Questions Hard Level Algebra questions basically involve modeling word problems into equations and then solving them. Some of the very basic formulae that come in handy while solving algebra questions are : (a + b) 2 = a 2 + b 2 + 2 a b(a - b) 2 = a 2 + b 2 - 2 a b(a + b) 2 - (a - b) 2 = 4 a b(a + b) 2 + (a - b) 2 = 2 ( 6 min read
• How to Graph Linear Inequalities Graphing linear inequalities is a fundamental skill in algebra that helps in visualizing the solutions to inequalities on the coordinate plane. This technique is essential for the solving systems of inequalities analyzing feasible regions in the optimization problems and understanding relationships 5 min read
• How to Solve Quadratic Inequalities Solving quadratic inequalities is a fundamental skill in algebra that helps you determine the range of values that satisfy a quadratic expression. This guide will walk you through the step-by-step process of solving quadratic inequalities effectively. Table of Content Quadratic Inequalities Definiti 5 min read
• Quadratic Inequalities Quadratic inequalities are a type of algebraic inequality that involves quadratic expressions. A quadratic inequality looks like ax2+bx+c>0, ax2+bx+c<0, ax2+bx+c≥0 or ax2+bx+c≤, where a, b, and c are constants, and a≠0. It is a fundamental concept in mathematics, particularly in algebra and ca 14 min read
• Multi-Step Inequalities Multi-step inequalities are similar to multi-step equations, but instead of finding the value of the variable that makes the equation true, you are finding a range of values that makes the inequality true. These types of inequalities involve more than one step to solve, typically requiring operation 6 min read
• Practice Problem on Linear Equations in Two Variables In this article, we will learn about one interesting topic which is covered in class 9 and class 10 mathematics. We will look at some formulas and problems of Linear equations in two variables. Important Formulas on Linear Equations in Two VariablesLinear equations in two variables are expressed in 8 min read
• Equations Reducible to Linear Form Equations Reducible to Linear Form" refers to equations that can be transformed or rewritten into a linear equation. These equations typically involve variables raised to powers other than 1, such as squared terms, cubed terms, or higher. By applying suitable substitutions or transformations, these 9 min read
• Algebra - Aptitude Questions and Answers Algebra is the basis for calculus, geometry, trigonometry, and statistics. This would require practicing as many questions as possible. These algebra Questions should cover a range of topics, including linear equations, quadratic equations, polynomials, etc Prerequisites: Algebra in Math Aptitude Qu 12 min read
• Inequalities in LaTeX LaTeX, a powerful typesetting system, is essential for producing high-quality scientific and technical documents. LaTeX excels in handling complex mathematical equations, references, and bibliographies, making it the go-to choice for researchers, engineers, and scholars. LaTeX, known for its precisi 3 min read
• Expressions And Equations Expression and Equations are two important concepts of algebra in mathematics. We need to learn about expressions and equations to solve different types of easy and complex problems in both mathematics and real-life applications. expression is a combination of numbers, variables, and operators while 7 min read
• School Learning
• Practice Questions

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Parallelogram
• Quadrilateral
• Parallelepiped
• Tetrahedron
• Dodecahedron
• Rectangular Prism
• Fibonacci Sequence
• Golden Ratio
• Fraction Calculator
• Mixed Fraction Calculator
• Greatest Common Factor Calulator
• Decimal to Fraction Calculator
• Whole Numbers
• Rational Numbers
• Place Value
• Irrational Numbers
• Natural Numbers
• Binary Operation
• Numerator and Denominator
• Order of Operations (PEMDAS)
• Scientific Notation
• Triangular Number
• Complex Number
• Binary Number System
• Binomial Theorem
• Quartic Function
• Mathematical Induction
• Group Theory
• Modular Arithmetic
• Euler’s Number
• Inequalities
• De Morgan’s Laws
• Transcendental Numbers

Last modified on April 17th, 2024

Inequality Word Problems

Inequalities are common in our everyday life. They help us express relationships between quantities that are unequal. Writing and solving word problems involving them helps develop our problem-solving approach, understanding, logical reasoning, and analytical skills.

Here are the 4 main keywords commonly used to write mathematical expressions involving inequalities.   

• At least →  ‘greater than or equal to’
• More than → ‘greater than’
• No more than or at most → ‘less than or equal to’
• Less than → ‘less than’

To participate in the annual sports day, Mr. Adams would like to have nine students in each group. But fewer than 54 students are in class today, so Mr. Adams is unable to make as many full groups as he wants. How many full groups can Mr. Adams make? Write the inequality that describes the situation.

Let ‘x’ be the total number of groups Mr. Adams can make. Since each group has 9 students, the total number of students in ‘x’ groups is 9x As we know, fewer than 54 students are in a class today. Thus, the inequality that represents the situation is: 9x < 54 On dividing both sides by 9, the maximum number of groups Mr. Adams can make is  x < 6 Thus, Mr. Adams can make a maximum of 6 full groups.

 Bruce needs at least \$561 to buy a new tablet. He has already saved \$121 and earns \$44 per month as a part-timer in a company. Write the inequality and determine how long he has to work to buy the tablet.

Let ‘x’ be the number of months Bruce needs to work. As we know,  The amount already saved by Bruce is \$121 He earns \$44 per month The cost of the tablet is at least \$561 After ‘x’ months of work, Bruce will have \$(121 + 44x) Now, the inequality representing the situation is: 121 + 44x ≥ 561 On subtracting 121 from both sides, 121 + 44x – 121 ≥ 561 – 121 ⇒ 44x ≥ 440 On dividing both sides by 44, x ≥ 10 Thus, Bruce needs to work for at least 10 months to buy the new tablet.

A store is offering a \$26 discount on all women’s clothes. Ava is looking at clothes originally priced between \$199 and \$299. How much can she expect to spend after the discount?

Let ‘x’ be the original price of the clothes Ava chooses. As we know, the original price range is 199 ≤ x ≤ 299, and the discount is \$26 Now, Ava pays \$(x – 26) after the discount. Thus, the inequality is: 199 – 26 ≤ x – 26 ≤ 299 – 26 ⇒ 173 ≤ x – 26 ≤ 273 Thus, she can expect to spend between \$173 and \$273 after the discount.

A florist makes a profit of \$6.25 per plant. If the store wants to profit at least \$4225, how many plants does it need to sell?

Let ‘P’ be the profit, ‘p’ be the profit per plant, and ‘n’ be the number of plants.  As we know, the store wants a profit of at least \$4225, and the florist makes a profit of \$6.25 per plant. Here, P ≥ 4225 and p = 6.25 …..(i) Also, P = p × n Substituting the values of (i), we get 6.25 × n ≥ 4225 On dividing both sides by 6.25, we get ${n\geq \dfrac{4225}{6\cdot 25}}$ ⇒ ${n\geq 676}$ Thus, the store needs to sell at least 676 plants to make a profit of \$4225.

Daniel had \$1200 in his savings account at the start of the year, but he withdraws \$60 each month to spend on transportation. He wants to have at least \$300 in the account at the end of the year. How many months can Daniel withdraw money from the account?

As we know, Daniel had \$1200 in his savings account at the start of the year, but he withdrew \$60 for transportation each month.  Thus, after ‘n’ months, he will have \$(1200−60n) left in his account. Also, Daniel wants to have at least \$300 in the account at the end of the year.  Here, the inequality is: 1200 – 60n ≥ 300 ⇒ 1200 – 60n – 1200 ≥ 300 – 1200 (by subtraction property) ⇒ -60n ≥ -900 ⇒ 60n ≤ 900 (by inversion property) ⇒ n ≤ ${\dfrac{900}{60}}$ ⇒ n ≤ 15 Thus, Daniel can withdraw money from the account for at most 15 months.

Anne is a model trying to lose weight for an upcoming beauty pageant. She currently weighs 165 lb. If she cuts 2 lb per week, how long will it take her to weigh less than 155 lb?

Let ‘t’ be the number of weeks to weigh less than 155 lb. As we know, Anne initially weighs 165 lb After ‘t’ weeks of cutting 2 lb per week, her weight will be 165 – 2t Now, Anne’s weight will be less than 155 lb Here, the inequality from the given word problem is: 165 – 2t < 155 On subtracting 165 from both sides, we get 165 – 2t – 165 < 155 – 165 ⇒ – 2t < -10 On dividing by -2, the inequality sign is reversed. ${\dfrac{-2t}{-2} >\dfrac{-10}{-2}}$ ⇒ t > 5

Rory and Cinder are on the same debate team. In one topic, Rory scored 5 points more than Cinder, but they scored less than 19 together. What are the possible points Rory scored?

Let Rory’s score be ‘r,’ and Cinder’s score be ‘c.’ As we know, Rory scored 5 points more than Cinder. Thus, Rory’s score is r = c + 5 …..(i) Also, their scores sum up to less than 19 points. Thus, the inequality is: r + c < 19 …..(ii) Substituting (i) in (ii), we get (c + 5) + c < 19 ⇒ 2c + 5 < 19 On subtracting 5 from both sides, we get 2c + 5 – 5 < 19 – 5 ⇒ 2c < 14 On dividing both sides by 2, we get ${\dfrac{2c}{2} >\dfrac{14}{2}}$ ⇒ c < 7 means Cinder’s score is less than 7 points. Now, from (i), r = c + 5 ⇒ c = r – 5 Thus, c < 7 ⇒ r – 5 < 7 On adding 5 to both sides, we get r – 5 + 5 < 7 + 5 ⇒ r < 12 means Rory’s score is less than 12 points. Hence, Rory’s scores can be 6, 7, 8, 9, 10, or 11 points.

An average carton of juice cans contains 74 pieces, but the number can vary by 4. Find out the maximum and minimum number of cans that can be present in a carton.

Let ‘c’ be the number of juice cans in a carton. As we know, the average number of cans in a carton is 74, and it varies by 4 cans. Thus, the required inequality is |c – 74| ≤ 4 ⇒ -4 ≤ c – 74 ≤ 4 On adding 74 to each side, we get -4 + 74 ≤ c – 74 + 74 ≤ 4 + 74 ⇒ 70 ≤ c ≤ 78 Hence, the minimum number of cans in a carton is 70, and the maximum number is 78.

 Layla rehearses singing for at least 12 hours per week, for three-fourths of an hour each session. If she has already sung 3 hours this week, how many more sessions remain for her to exceed her weekly practice goal?

Let ‘p’ be Layla’s total hours of practice in a week, and ‘s’ be the number of sessions she needs to complete. As we know, Layla has already rehearsed 3 hours, then her remaining rehearsal time is (p – 3) Each session lasts for three-fourths of an hour. Thus, we have the inequality: ${\dfrac{3}{4}s >p-3}$ …..(i) As we know, Layla rehearses for at least 12 hours, which means p ≥ 12 …..(ii) From (i), ${\dfrac{3}{4}s >p-3}$ ⇒ ${s >\dfrac{4}{3}\left( p-3\right)}$ From (ii), substituting the value p = 12 in (i), we get ${s >\dfrac{4}{3}\left( 12-3\right)}$ ⇒ ${s >\dfrac{4}{3}\cdot 9}$ ⇒ s > 12 Thus, Layla must complete more than 12 sessions to exceed her weekly rehearsal goal.

• Privacy Policy
• Trigonometry

Join Our Newsletter

© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Solving inequalities

Here you will learn about solving inequalities, including how to solve linear inequalities, identify integers in the solution set, and represent solutions on a number line.

Students will first learn about solving simple inequalities as part of expressions and equations in 6th grade math and expand that knowledge in 7th grade math.

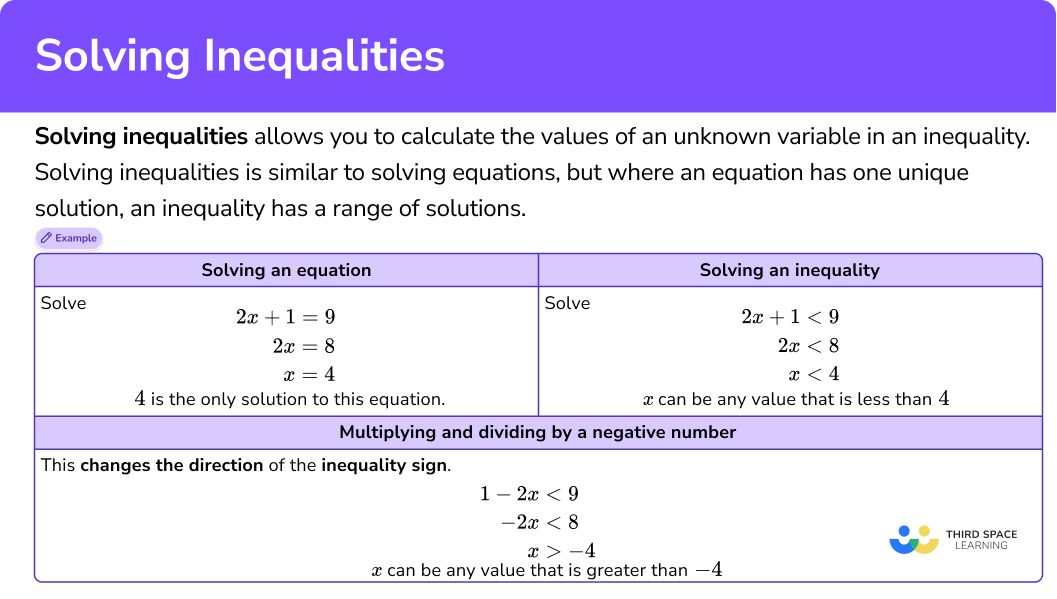
What is solving inequalities?

Solving inequalities allows you to calculate the values of an unknown variable in an inequality.

Solving inequalities is similar to solving equations, but where an equation has one unique solution, an inequality has a range of solutions.

In order to solve an inequality, you need to balance the inequality on each side of the inequality sign in the same way as you would balance an equation on each side of the equal sign. Solutions can be integers, decimals, positive numbers, or negative numbers.

For example,

[FREE] Solving Inequalities Worksheet (Grade 7)

Use this worksheet to check your 7th grade students’ understanding of solving inequalities. 15 questions with answers to identify areas of strength and support!

Common Core State Standards

How does this relate to 6th grade and 7th grade math?

• Grade 6 – Expressions and Equations (6.EE.B.8) Write an inequality of the form x > c or x < c to represent a constraint or condition in a real-world or mathematical problem. Recognize that inequalities of the form x > c or x < c have infinitely many solutions; represent solutions of such inequalities on number line diagrams.
• Grade 7 – Expressions and Equations (7.EE.4b) Solve word problems leading to inequalities of the form px + q > r or px + q < r, where p, q, and r are specific rational numbers. Graph the solution set of the inequality and interpret it in the context of the problem. For example: As a salesperson, you are paid \$50 per week plus \$3 per sale. This week you want your pay to be at least \$100. Write an inequality for the number of sales you need to make, and describe the solutions.

How to solve inequalities

In order to solve inequalities:

Rearrange the inequality so that all the unknowns are on one side of the inequality sign.

Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.

Write your solution with the inequality symbol.

Solving linear inequalities examples

Example 1: solving linear inequalities.

4 x+6<26

In this case you are subtracting 6 from both sides.

\begin{aligned} 4x+6&<26\\ 4x&<20 \end{aligned}

This leaves 4x on the left side of the inequality sign and 20 on the right side.

2 Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.

In this case you need to divide both sides by 4.

\begin{aligned} 4x&<20\\ x&<5 \end{aligned}

This leaves x on the left side of the inequality sign and 5 on the right side.

3 Write your solution with the inequality symbol.

Any value less than 5 satisfies the inequality.

Example 2: solving linear inequalities

5x-4 \geq 26

In this case you need to add 4 to both sides.

\begin{aligned} 5x-4&\geq26\\ 5x&\geq30 \end{aligned}

This leaves 5x on the left side of the inequality sign and 30 on the right side.

In this case you need to divide both sides by 5.

\begin{aligned} 5x&\geq30\\ x&\geq6 \end{aligned}

This leaves x on the left side of the inequality sign and 6 on the right side.

Any value greater than or equal to 6 satisfies the inequality.

Example 3: solving linear inequalities with parentheses

3(x-4)\leq12

Let’s start by expanding the parentheses.

3x-12\leq12

Then you need to add 12 to both sides.

\begin{aligned} 3x-12&\leq12\\ 3x&\leq24 \end{aligned}

This leaves 3x on the left side of the inequality sign and 24 on the right side.

In this case you need to divide both sides by 3.

\begin{aligned} 3x&\leq24\\ x&\leq8 \end{aligned}

This leaves x on the left side of the inequality sign and 8 on the right side.

Any value less than or equal to 8 satisfies the inequality.

Example 4: solving linear inequalities with unknowns on both sides

5x-6 > 2x + 15

In this case you need to subtract 2x from both sides.

\begin{aligned} 5x-6&>2x+15\\ 3x-6&>15 \end{aligned}

This leaves 3x-6 on the left side of the inequality sign and 15 on the right side.

Rearrange the inequality so that \textbf{‘x’} s are on one side of the inequality sign and numbers on the other.

In this case you need to add 6 to both sides.

\begin{aligned} 3x-6&>15\\ 3x&>21 \end{aligned}

This leaves 3x on the left side of the inequality sign and 21 on the right side.

\begin{aligned} 3x&>21\\ x&>7 \end{aligned}

This leaves x on the left side of the inequality sign and 7 on the right side.

Any value greater than 7 satisfies the inequality.

Example 5: solving linear inequalities with fractions

\cfrac{x+3}{5}<2

Rearrange the inequality to eliminate the denominator.

In this case you need to multiply both sides by 5.

\begin{aligned} \cfrac{x+3}{5}&<2\\ x+3&<10 \end{aligned}

In this case you need to subtract 3 from both sides.

\begin{aligned} \cfrac{x+3}{5}&<2\\ x+3&<10\\ x&<7 \end{aligned}

Any value less than 7 satisfies the inequality.

Example 6: solving linear inequalities with non-integer solutions

In this case you need to subtract 6 from both sides.

\begin{aligned} 6x+1&\geq4\\ 6x&\geq3 \end{aligned}

In this case you need to divide both sides by 6.

\begin{aligned} 6x+1&\geq4\\ 6x&\geq3\\ x&\geq\cfrac{3}{6} \end{aligned}

This can be simplified to \, \cfrac{1}{2} \, or the decimal equivalent.

x\geq\cfrac{1}{2}

Any value greater than or equal to \, \cfrac{1}{2} \, satisfies the inequality.

Example 7: solving linear inequalities and representing solutions on a number line

Represent the solution on a number line:

2x-7 < 5

In this case you need to add 7 to both sides.

\begin{aligned} 2x-7&<5\\ 2x&<12 \end{aligned}

In this case you need to divide both sides by 2.

\begin{aligned} 2x-7& <5\\ 2x& <12\\ x& < 6 \end{aligned}

Represent your solution on a number line.

Any value less than 6 satisfies the inequality. An open circle is required at 6 and the values lower than 6 indicated with an arrow.

Example 8: solving linear inequalities with negative x coefficients

In this case you need to subtract 1 from both sides.

\begin{aligned} 1-2x & <7 \\ -2x & <6 \end{aligned}

In this case you need to divide both sides by negative 2.

6 \div-2=-3

Change the direction of the inequality sign.

Because you divided by a negative number, you also need to change the direction of the inequality sign.

\begin{aligned} 1-2x & <7 \\ -2x & <6 \\ x &>-3 \end{aligned}

Example 9: solving linear inequalities and listing integer values that satisfy the inequality

List the integer values that satisfy:

3 < x+1\leq8

In this case you need to subtract 1 from each part.

\begin{aligned} 3&<x+1\leq8\\ 2&<x\leq7\\ \end{aligned}

List the integer values satisfied by the inequality.

2<x\leq7

2 is not included in the solution set. 7 is included in the solution set. The integers that satisfy this inequality are:

3, 4, 5, 6, 7

Example 10: solving linear inequalities and listing integer values that satisfy the inequality

7\leq4x\leq20

In this case you need to divide each part by 4.

\begin{aligned} 7\leq \, & 4x\leq20\\ \cfrac{7}{4}\leq & \; x \leq5 \end{aligned}

\cfrac{7}{4} \leq x \leq 5

\cfrac{7}{4} \, is included in the solution set but it is not an integer.

The first integer higher is 2.

5 is also included in the solution set.

The integers that satisfy this inequality are:

Example 11: solving linear inequalities and representing the solution on a number line

-3<2x+5\leq7

In this case you need to subtract 5 from each part.

\begin{aligned} -3<2x+5&\leq7\\ -8<2x&\leq2 \end{aligned}

Rearrange the inequality so that \textbf{‘x’} is isolated. In this case you need to divide each part by \bf{2} .

\begin{aligned} -3<2x+5&\leq7\\ -8<2x&\leq2\\ -4<x&\leq1 \end{aligned}

Represent the solution set on a the number line

-4<x\leq1

-4 is not included in the solution set so requires an open circle. 1 is included in the solution set so requires a closed circle.

Put a solid line between the circles to indicate all the values that satisfy the solution set.

Teaching tips for solving inequalities

• Students should master solving simple inequalities (one-step inequalities) before moving on to two-step inequalities (or multi-step inequalities).
• Foster student engagement by practicing solving inequalities through classroom games such as BINGO rather than daily worksheets.
• Student practice problems should have a variety of inequalities such as inequalities with fractions, negative numbers, and parentheses. (see examples above)

Easy mistakes to make

• Solutions as inequalities Not including the inequality symbol in the solution is a common mistake. An inequality has a range of values that satisfy it rather than a unique solution so the inequality symbol is essential. For example, when solving x + 3 < 7 giving a solution of 4 or x = 4 is incorrect, the answer must be written as an inequality x < 4 .
• Balancing inequalities Errors can be made with solving equations and inequalities by not applying inverse operations or not balancing the inequalities. Work should be shown step-by-step with the inverse operations applied to both sides of the inequality. For example, when solving x + 3 < 7 , adding 3 to both sides rather than subtracting 3 from both sides.

Related inequalities lessons

• Inequalities
• Linear inequalities
• Inequalities on a number line
• Graphing inequalities
• Quadratic inequalities
• Greater than sign
• Less than sign

Practice solving inequalities questions

3x+7 < 31

\begin{aligned} 3x+7&<31\\ 3x&<24\\ x&<8 \end{aligned}

\begin{aligned} 4x-3&\geq25\\ 4x&\geq28\\ x&\geq7 \end{aligned}

2(x-5)\leq8

\begin{aligned} 2(x-5)&\leq8\\ 2x-10&\leq8\\ 2x&\leq18\\ x&\leq9 \end{aligned}

6x-5 > 4x + 1

\begin{aligned} 6x-5&>4x+1\\ 2x-5&>1\\ 2x&>6\\ x&>3 \end{aligned}

\cfrac{x-4}{2}>6

\begin{aligned} \cfrac{x-4}{2}&>6\\ x-4&>12\\ x&>16 \end{aligned}

\begin{aligned} 8x+1&\geq3\\ 8x&\geq2\\ x&\geq\cfrac{2}{8}\\ x&\geq\cfrac{1}{4} \end{aligned}

7. Represent the solution on a number line.

5x-2 < 28

\begin{aligned} 5x-2&<28\\ 5x&<30\\ x&<6 \end{aligned}

An open circle is required and all values less than 6 indicated.

2-3x > 14

\begin{aligned} 2-3x &>14 \\ -3x &>12 \\ x &< -4 \end{aligned}

Change the direction of the inequality sign as you have divided by a negative number.

9. List the integer values that satisfy:

2<x+3\leq5

\begin{aligned} 2<x&+3\leq5\\ -1< \, &x\leq2 \end{aligned}

-1 is not included in the solution set as is greater than -1.

2 is included in the solution set as x is less than or equal to 2.

10. List the integer values that satisfy:

4\leq3x\leq21

\begin{aligned} 4\leq3&x\leq21\\ \cfrac{4}{3} \, \leq \, &x\leq7 \end{aligned}

The first integer greater than \, \cfrac{4}{3} \, is 2.

7 is included in the solution set as x is less than or equal to 7.

11. List the integer values that satisfy:

-4<3x+2\leq5

\begin{aligned} -4<3x&+2\leq5\\ -6<3&x\leq3\\ -2< \, &x\leq1 \end{aligned}

-2 is not included in the solution set as x is greater than -2.

1 is included in the solution set as x is less than or equal to 1.

Solving inequalities FAQs

Solving inequalities is where you calculate the values that an unknown variable can be in an inequality.

To solve an inequality, you need to balance the inequality on each side of the inequality sign in the same way as you would balance an equation on each side of the equal sign. Solutions can be integers, decimals, positive numbers, or negative numbers.

The next lessons are

• Types of graphs
• Math formulas
• Coordinate plane

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview