hypothesis testing using python

What Is Hypothesis Testing? Types and Python Code Example

Curiosity has always been a part of human nature. Since the beginning of time, this has been one of the most important tools for birthing civilizations. Still, our curiosity grows — it tests and expands our limits. Humanity has explored the plains of land, water, and air. We've built underwater habitats where we could live for weeks. Our civilization has explored various planets. We've explored land to an unlimited degree.

These things were possible because humans asked questions and searched until they found answers. However, for us to get these answers, a proven method must be used and followed through to validate our results. Historically, philosophers assumed the earth was flat and you would fall off when you reached the edge. While philosophers like Aristotle argued that the earth was spherical based on the formation of the stars, they could not prove it at the time.

This is because they didn't have adequate resources to explore space or mathematically prove Earth's shape. It was a Greek mathematician named Eratosthenes who calculated the earth's circumference with incredible precision. He used scientific methods to show that the Earth was not flat. Since then, other methods have been used to prove the Earth's spherical shape.

When there are questions or statements that are yet to be tested and confirmed based on some scientific method, they are called hypotheses. Basically, we have two types of hypotheses: null and alternate.

A null hypothesis is one's default belief or argument about a subject matter. In the case of the earth's shape, the null hypothesis was that the earth was flat.

An alternate hypothesis is a belief or argument a person might try to establish. Aristotle and Eratosthenes argued that the earth was spherical.

Other examples of a random alternate hypothesis include:

The weather may have an impact on a person's mood.
More people wear suits on Mondays compared to other days of the week.
Children are more likely to be brilliant if both parents are in academia, and so on.

What is Hypothesis Testing?

Hypothesis testing is the act of testing whether a hypothesis or inference is true. When an alternate hypothesis is introduced, we test it against the null hypothesis to know which is correct. Let's use a plant experiment by a 12-year-old student to see how this works.

The hypothesis is that a plant will grow taller when given a certain type of fertilizer. The student takes two samples of the same plant, fertilizes one, and leaves the other unfertilized. He measures the plants' height every few days and records the results in a table.

After a week or two, he compares the final height of both plants to see which grew taller. If the plant given fertilizer grew taller, the hypothesis is established as fact. If not, the hypothesis is not supported. This simple experiment shows how to form a hypothesis, test it experimentally, and analyze the results.

In hypothesis testing, there are two types of error: Type I and Type II.

When we reject the null hypothesis in a case where it is correct, we've committed a Type I error. Type II errors occur when we fail to reject the null hypothesis when it is incorrect.

In our plant experiment above, if the student finds out that both plants' heights are the same at the end of the test period yet opines that fertilizer helps with plant growth, he has committed a Type I error.

However, if the fertilized plant comes out taller and the student records that both plants are the same or that the one without fertilizer grew taller, he has committed a Type II error because he has failed to reject the null hypothesis.

What are the Steps in Hypothesis Testing?

The following steps explain how we can test a hypothesis:

Step #1 - Define the Null and Alternative Hypotheses

Before making any test, we must first define what we are testing and what the default assumption is about the subject. In this article, we'll be testing if the average weight of 10-year-old children is more than 32kg.

Our null hypothesis is that 10 year old children weigh 32 kg on average. Our alternate hypothesis is that the average weight is more than 32kg. Ho denotes a null hypothesis, while H1 denotes an alternate hypothesis.

Step #2 - Choose a Significance Level

The significance level is a threshold for determining if the test is valid. It gives credibility to our hypothesis test to ensure we are not just luck-dependent but have enough evidence to support our claims. We usually set our significance level before conducting our tests. The criterion for determining our significance value is known as p-value.

A lower p-value means that there is stronger evidence against the null hypothesis, and therefore, a greater degree of significance. A p-value of 0.05 is widely accepted to be significant in most fields of science. P-values do not denote the probability of the outcome of the result, they just serve as a benchmark for determining whether our test result is due to chance. For our test, our p-value will be 0.05.

Step #3 - Collect Data and Calculate a Test Statistic

You can obtain your data from online data stores or conduct your research directly. Data can be scraped or researched online. The methodology might depend on the research you are trying to conduct.

We can calculate our test using any of the appropriate hypothesis tests. This can be a T-test, Z-test, Chi-squared, and so on. There are several hypothesis tests, each suiting different purposes and research questions. In this article, we'll use the T-test to run our hypothesis, but I'll explain the Z-test, and chi-squared too.

T-test is used for comparison of two sets of data when we don't know the population standard deviation. It's a parametric test, meaning it makes assumptions about the distribution of the data. These assumptions include that the data is normally distributed and that the variances of the two groups are equal. In a more simple and practical sense, imagine that we have test scores in a class for males and females, but we don't know how different or similar these scores are. We can use a t-test to see if there's a real difference.

The Z-test is used for comparison between two sets of data when the population standard deviation is known. It is also a parametric test, but it makes fewer assumptions about the distribution of data. The z-test assumes that the data is normally distributed, but it does not assume that the variances of the two groups are equal. In our class test example, with the t-test, we can say that if we already know how spread out the scores are in both groups, we can now use the z-test to see if there's a difference in the average scores.

The Chi-squared test is used to compare two or more categorical variables. The chi-squared test is a non-parametric test, meaning it does not make any assumptions about the distribution of data. It can be used to test a variety of hypotheses, including whether two or more groups have equal proportions.

Step #4 - Decide on the Null Hypothesis Based on the Test Statistic and Significance Level

After conducting our test and calculating the test statistic, we can compare its value to the predetermined significance level. If the test statistic falls beyond the significance level, we can decide to reject the null hypothesis, indicating that there is sufficient evidence to support our alternative hypothesis.

On the other contrary, if the test statistic does not exceed the significance level, we fail to reject the null hypothesis, signifying that we do not have enough statistical evidence to conclude in favor of the alternative hypothesis.

Step #5 - Interpret the Results

Depending on the decision made in the previous step, we can interpret the result in the context of our study and the practical implications. For our case study, we can interpret whether we have significant evidence to support our claim that the average weight of 10 year old children is more than 32kg or not.

For our test, we are generating random dummy data for the weight of the children. We'll use a t-test to evaluate whether our hypothesis is correct or not.

For a better understanding, let's look at what each block of code does.

The first block is the import statement, where we import numpy and scipy.stats . Numpy is a Python library used for scientific computing. It has a large library of functions for working with arrays. Scipy is a library for mathematical functions. It has a stat module for performing statistical functions, and that's what we'll be using for our t-test.

The weights of the children were generated at random since we aren't working with an actual dataset. The random module within the Numpy library provides a function for generating random numbers, which is randint .

The randint function takes three arguments. The first (20) is the lower bound of the random numbers to be generated. The second (40) is the upper bound, and the third (100) specifies the number of random integers to generate. That is, we are generating random weight values for 100 children. In real circumstances, these weight samples would have been obtained by taking the weight of the required number of children needed for the test.

Using the code above, we declared our null and alternate hypotheses stating the average weight of a 10-year-old in both cases.

t_stat and p_value are the variables in which we'll store the results of our functions. stats.ttest_1samp is the function that calculates our test. It takes in two variables, the first is the data variable that stores the array of weights for children, and the second (32) is the value against which we'll test the mean of our array of weights or dataset in cases where we are using a real-world dataset.

The code above prints both values for t_stats and p_value .

Lastly, we evaluated our p_value against our significance value, which is 0.05. If our p_value is less than 0.05, we reject the null hypothesis. Otherwise, we fail to reject the null hypothesis. Below is the output of this program. Our null hypothesis was rejected.

In this article, we discussed the importance of hypothesis testing. We highlighted how science has advanced human knowledge and civilization through formulating and testing hypotheses.

We discussed Type I and Type II errors in hypothesis testing and how they underscore the importance of careful consideration and analysis in scientific inquiry. It reinforces the idea that conclusions should be drawn based on thorough statistical analysis rather than assumptions or biases.

We also generated a sample dataset using the relevant Python libraries and used the needed functions to calculate and test our alternate hypothesis.

Thank you for reading! Please follow me on LinkedIn where I also post more data related content.

Adventures in Machine Learning

Mastering hypothesis testing in python: a step-by-step guide, hypothesis testing in python.

Hypothesis testing is a statistical technique that allows us to draw conclusions about a population based on a sample of data. It is often used in fields like medicine, psychology, and economics to test the effectiveness of new treatments, analyze consumer behavior, or estimate the impact of policy changes.

In Python, hypothesis testing is facilitated by modules such as scipy.stats and statsmodels.stats . In this article, we’ll explore three examples of hypothesis testing in Python: the one sample t-test, the two sample t-test, and the paired samples t-test.

For each test, we’ll provide a brief explanation of the underlying concepts, an example of a research question that can be answered using the test, and a step-by-step guide to performing the test in Python. Let’s get started!

One Sample t-test

The one sample t-test is used to compare a sample mean to a known or hypothesized population mean. This allows us to determine whether the sample mean is significantly different from the population mean.

The test assumes that the data are normally distributed and that the sample is randomly drawn from the population. Example research question: Is the mean weight of a species of turtle significantly different from a known or hypothesized value?

Step-by-step guide:

Define the null hypothesis (H0) and alternative hypothesis (Ha).

The null hypothesis is typically that the sample mean is equal to the population mean. The alternative hypothesis is that they are not equal.

For example:

H0: The mean weight of a species of turtle is 100 grams. Ha: The mean weight of a species of turtle is not 100 grams.

Collect a random sample of data.

This can be done using Python’s random module or by importing data from a file. For example:

weight_sample = [95, 105, 110, 98, 102, 116, 101, 99, 104, 108]

Calculate the sample mean (x), sample standard deviation (s), and standard error (SE).

x = sum(weight_sample)/len(weight_sample) s = np.std(weight_sample) SE = s / (len(weight_sample)**0.5)

Calculate the t-value using the formula: t = (x - μ) / (SE) , where μ is the hypothesized population mean.

t = (x - 100) / SE

Calculate the p-value using a t-distribution table or a Python function like scipy.stats.ttest_1samp() .

p_value = scipy.stats.ttest_1samp(weight_sample, 100).pvalue

Compare the p-value to the level of significance (α), typically set to 0.05.

If the p-value is less than α, reject the null hypothesis and conclude that there is sufficient evidence to support the alternative hypothesis.

If the p-value is greater than α, fail to reject the null hypothesis and conclude that there is insufficient evidence to support the alternative hypothesis. For example:

Two Sample t-test

The two sample t-test is used to compare the means of two independent samples. This allows us to determine whether the means are significantly different from each other.

The test assumes that the data are normally distributed and that the samples are randomly drawn from their respective populations. Example research question: Is the mean weight of two different species of turtles significantly different from each other?

The null hypothesis is typically that the sample means are equal. The alternative hypothesis is that they are not equal.

H0: The mean weight of species A is equal to the mean weight of species B. Ha: The mean weight of species A is not equal to the mean weight of species B.

Collect two random samples of data.

This can be done using Python's random module or by importing data from a file. For example:

species_a = [95, 105, 110, 98, 102] species_b = [116, 101, 99, 104, 108]

Calculate the sample means (x1, x2), sample standard deviations (s1, s2), and pooled standard error (SE).

x1 = sum(species_a)/len(species_a) x2 = sum(species_b)/len(species_b) s1 = np.std(species_a) s2 = np.std(species_b) n1 = len(species_a) n2 = len(species_b) SE = (((n1-1)*s1**2 + (n2-1)*s2**2)/(n1+n2-2))**0.5 * (1/n1 + 1/n2)**0.5

Calculate the t-value using the formula: t = (x1 - x2) / (SE) , where x1 and x2 are the sample means.

t = (x1 - x2) / SE

Calculate the p-value using a t-distribution table or a Python function like scipy.stats.ttest_ind() .

p_value = scipy.stats.ttest_ind(species_a, species_b).pvalue

Paired Samples t-test

The paired samples t-test is used to compare the means of two related samples. This allows us to determine whether the means are significantly different from each other, while accounting for individual differences between the samples.

The test assumes that the differences between paired observations are normally distributed. Example research question: Is there a significant difference in the max vertical jump of basketball players before and after a training program?

The null hypothesis is typically that the mean difference is equal to zero. The alternative hypothesis is that it is not equal to zero.

H0: The mean difference in max vertical jump before and after training is zero. Ha: The mean difference in max vertical jump before and after training is not zero.

Collect two related samples of data.

This can be done by measuring the same variable in the same subjects before and after a treatment or intervention. For example:

before = [72, 69, 77, 71, 76] after = [80, 70, 75, 74, 78]

Calculate the differences between the paired observations and the sample mean difference (d), sample standard deviation (s), and standard error (SE).

differences = [after[i]-before[i] for i in range(len(before))] d = sum(differences)/len(differences) s = np.std(differences) SE = s / (len(differences)**0.5)

Calculate the t-value using the formula: t = (d - μ) / (SE) , where μ is the hypothesized population mean difference (usually zero).

t = (d - 0) / SE

Calculate the p-value using a t-distribution table or a Python function like scipy.stats.ttest_rel() .

p_value = scipy.stats.ttest_rel(after, before).pvalue

Two Sample t-test in Python

The two sample t-test is used to compare two independent samples and determine if there is a significant difference between the means of the two populations. In this test, the null hypothesis is that the means of the two samples are equal, while the alternative hypothesis is that they are not equal.

Example research question: Is the mean weight of two different species of turtles significantly different from each other? Step-by-step guide:

Define the null hypothesis (H0) and alternative hypothesis (Ha). The null hypothesis is that the mean weight of the two turtle species is the same.

The alternative hypothesis is that they are not equal. For example:

H0: The mean weight of species A is equal to the mean weight of species B.

Ha: The mean weight of species A is not equal to the mean weight of species B. 2.

Collect a random sample of data for each species. For example:

species_a = [4.3, 3.9, 5.1, 4.6, 4.2, 4.8] species_b = [4.9, 5.2, 5.5, 5.3, 5.0, 4.7]

Calculate the sample mean (x1, x2), sample standard deviation (s1, s2), and pooled standard error (SE).

import numpy as np from scipy.stats import ttest_ind x1 = np.mean(species_a) x2 = np.mean(species_b) s1 = np.std(species_a) s2 = np.std(species_b) n1 = len(species_a) n2 = len(species_b) SE = np.sqrt(s1**2/n1 + s2**2/n2)

Calculate the p-value using a t-distribution table or a Python function like ttest_ind() .

p_value = ttest_ind(species_a, species_b).pvalue

If the p-value is less than α, reject the null hypothesis and conclude that there is sufficient evidence to support the alternative hypothesis. If the p-value is greater than α, fail to reject the null hypothesis and conclude that there is insufficient evidence to support the alternative hypothesis.

alpha = 0.05 if p_value print("Reject the null hypothesis.") else: print("Fail to reject the null hypothesis.")

In this example, if the p-value is less than 0.05, we would reject the null hypothesis and conclude that there is a significant difference between the mean weight of the two turtle species.

Paired Samples t-test in Python

The paired samples t-test is used to compare the means of two related samples. In this test, the null hypothesis is that the difference between the two means is equal to zero, while the alternative hypothesis is that they are not equal.

Example research question: Is there a significant difference in the max vertical jump of basketball players before and after a training program? Step-by-step guide:

Define the null hypothesis (H0) and alternative hypothesis (Ha). The null hypothesis is that the mean difference in max vertical jump before and after the training program is zero.

The alternative hypothesis is that it is not zero. For example:

H0: The mean difference in max vertical jump before and after the training program is zero.

Ha: The mean difference in max vertical jump before and after the training program is not zero. 2.

Collect two related samples of data, such as the max vertical jump of basketball players before and after a training program. For example:

before_training = [58, 64, 62, 70, 68] after_training = [62, 66, 64, 74, 70]

differences = [after_training[i]-before_training[i] for i in range(len(before_training))] d = np.mean(differences) s = np.std(differences) n = len(differences) SE = s / np.sqrt(n)

Calculate the p-value using a t-distribution table or a Python function like ttest_rel() .

p_value = ttest_rel(after_training, before_training).pvalue

if p_value print("Reject the null hypothesis.") else: print("Fail to reject the null hypothesis.")

In this example, if the p-value is less than 0.05, we would reject the null hypothesis and conclude that there is a significant difference in the max vertical jump of basketball players before and after the training program.

Hypothesis testing is an essential tool in statistical analysis, which gives us insights into populations based on limited data. The two sample t-test and paired samples t-test are two popular statistical methods that enable researchers to compare means of samples and determine whether they are significantly different.

With the help of Python, hypothesis testing in practice is made more accessible and convenient than ever before. In this article, we have provided a step-by-step guide to performing these tests in Python, enabling researchers to perform rigorous analyses that generate meaningful and accurate results.

In conclusion, hypothesis testing in Python is a crucial step in making conclusions about populations based on data samples. The three common hypothesis tests in Python; one-sample t-test, two-sample t-test, and paired samples t-test can be effectively applied to explore various research questions.

By setting null and alternative hypotheses, collecting data, calculating mean and standard deviation values, computing t-value, and comparing it with the set significance level of α, we can determine if there's enough evidence to reject the null hypothesis. With the use of such powerful methods, scientists can give more accurate and informed conclusions to real-world problems and take critical decisions when needed.

Continual learning and expertise with hypothesis testing in Python tools can enable researchers to leverage this powerful statistical tool for better outcomes.

Your Data Guide

Share this post.

How to Perform Hypothesis Testing Using Python

Step into the intriguing world of hypothesis testing, where your natural curiosity meets the power of data to reveal truths!

This article is your key to unlocking how those everyday hunches—like guessing a group’s average income or figuring out who owns their home—can be thoroughly checked and proven with data.

Thanks for reading Your Data Guide! Subscribe for free to receive new posts and support my work.

I am going to take you by the hand and show you, in simple steps, how to use Python to explore a hypothesis about the average yearly income.

By the time we’re done, you’ll not only get the hang of creating and testing hypotheses but also how to use statistical tests on actual data.

Perfect for up-and-coming data scientists, anyone with a knack for analysis, or just if you’re keen on data, get ready to gain the skills to make informed decisions and turn insights into real-world actions.

Join me as we dive deep into the data, one hypothesis at a time!

Before we get started, elevate your data skills with my expert eBooks—the culmination of my experiences and insights.

Support my work and enhance your journey. Check them out:

eBook 1: Personal INTERVIEW Ready “SQL” CheatSheet

eBook 2: Personal INTERVIEW Ready “Statistics” Cornell Notes

Best Selling eBook: Top 50+ ChatGPT Personas for Custom Instructions

Data Science Bundle ( Cheapest ): The Ultimate Data Science Bundle: Complete

ChatGPT Bundle ( Cheapest ): The Ultimate ChatGPT Bundle: Complete

💡 Checkout for more such resources: https://codewarepam.gumroad.com/

What is a hypothesis, and how do you test it?

A hypothesis is like a guess or prediction about something specific, such as the average income or the percentage of homeowners in a group of people.

It’s based on theories, past observations, or questions that spark our curiosity.

For instance, you might predict that the average yearly income of potential customers is over $50,000 or that 60% of them own their homes.

To see if your guess is right, you gather data from a smaller group within the larger population and check if the numbers ( like the average income, percentage of homeowners, etc. ) from this smaller group match your initial prediction.

You also set a rule for how sure you need to be to trust your findings, often using a 5% chance of error as a standard measure . This means you’re 95% confident in your results. — Level of Significance (0.05)

There are two main types of hypotheses : the null hypothesi s, which is your baseline saying there’s no change or difference, and the alternative hypothesis , which suggests there is a change or difference.

For example,

If you start with the idea that the average yearly income of potential customers is $50,000,

The alternative could be that it’s not $50,000—it could be less or more, depending on what you’re trying to find out.

To test your hypothesis, you calculate a test statistic —a number that shows how much your sample data deviates from what you predicted.

How you calculate this depends on what you’re studying and the kind of data you have. For example, to check an average, you might use a formula that considers your sample’s average, the predicted average, the variation in your sample data, and how big your sample is.

This test statistic follows a known distribution ( like the t-distribution or z-distribution ), which helps you figure out the p-value.

The p-value tells you the odds of seeing a test statistic as extreme as yours if your initial guess was correct.

A small p-value means your data strongly disagrees with your initial guess.

Finally, you decide on your hypothesis by comparing the p-value to your error threshold.

If the p-value is smaller or equal, you reject the null hypothesis, meaning your data shows a significant difference that’s unlikely due to chance.

If the p-value is larger, you stick with the null hypothesis , suggesting your data doesn’t show a meaningful difference and any change might just be by chance.

We’ll go through an example that tests if the average annual income of prospective customers exceeds $50,000.

This process involves stating hypotheses , specifying a significance level , collecting and analyzing data , and drawing conclusions based on statistical tests.

Example: Testing a Hypothesis About Average Annual Income

Step 1: state the hypotheses.

Null Hypothesis (H0): The average annual income of prospective customers is $50,000.

Alternative Hypothesis (H1): The average annual income of prospective customers is more than $50,000.

Step 2: Specify the Significance Level

Significance Level: 0.05, meaning we’re 95% confident in our findings and allow a 5% chance of error.

Step 3: Collect Sample Data

We’ll use the ProspectiveBuyer table, assuming it's a random sample from the population.

This table has 2,059 entries, representing prospective customers' annual incomes.

Step 4: Calculate the Sample Statistic

In Python, we can use libraries like Pandas and Numpy to calculate the sample mean and standard deviation.

SampleMean: 56,992.43

SampleSD: 32,079.16

SampleSize: 2,059

Step 5: Calculate the Test Statistic

We use the t-test formula to calculate how significantly our sample mean deviates from the hypothesized mean.

Python’s Scipy library can handle this calculation:

T-Statistic: 4.62

Step 6: Calculate the P-Value

The p-value is already calculated in the previous step using Scipy's ttest_1samp function, which returns both the test statistic and the p-value.

P-Value = 0.0000021

Step 7: State the Statistical Conclusion

We compare the p-value with our significance level to decide on our hypothesis:

Since the p-value is less than 0.05, we reject the null hypothesis in favor of the alternative.

Conclusion:

There’s strong evidence to suggest that the average annual income of prospective customers is indeed more than $50,000.

This example illustrates how Python can be a powerful tool for hypothesis testing, enabling us to derive insights from data through statistical analysis.

How to Choose the Right Test Statistics

Choosing the right test statistic is crucial and depends on what you’re trying to find out, the kind of data you have, and how that data is spread out.

Here are some common types of test statistics and when to use them:

T-test statistic:

This one’s great for checking out the average of a group when your data follows a normal distribution or when you’re comparing the averages of two such groups.

The t-test follows a special curve called the t-distribution . This curve looks a lot like the normal bell curve but with thicker ends, which means more chances for extreme values.

The t-distribution’s shape changes based on something called degrees of freedom , which is a fancy way of talking about your sample size and how many groups you’re comparing.

Z-test statistic:

Use this when you’re looking at the average of a normally distributed group or the difference between two group averages, and you already know the standard deviation for all in the population.

The z-test follows the standard normal distribution , which is your classic bell curve centered at zero and spreading out evenly on both sides.

Chi-square test statistic:

This is your go-to for checking if there’s a difference in variability within a normally distributed group or if two categories are related.

The chi-square statistic follows its own distribution, which leans to the right and gets its shape from the degrees of freedom —basically, how many categories or groups you’re comparing.

F-test statistic:

This one helps you compare the variability between two groups or see if the averages of more than two groups are all the same, assuming all groups are normally distributed.

The F-test follows the F-distribution , which is also right-skewed and has two types of degrees of freedom that depend on how many groups you have and the size of each group.

In simple terms, the test you pick hinges on what you’re curious about, whether your data fits the normal curve, and if you know certain specifics, like the population’s standard deviation.

Each test has its own special curve and rules based on your sample’s details and what you’re comparing.

Join my community of learners! Subscribe to my newsletter for more tips, tricks, and exclusive content on mastering Data Science & AI. — Your Data Guide Join my community of learners! Subscribe to my newsletter for more tips, tricks, and exclusive content on mastering data science and AI. By Richard Warepam ⭐️ Visit My Gumroad Shop: https://codewarepam.gumroad.com/

Discussion about this post

Ready for more?

Visual Design.

Upgrade to get unlimited access ($10 one off payment).

7 Tips for Beginner to Future-Proof your Machine Learning Project

LLM Prompt Engineering Techniques for Knowledge Graph Integration

Develop a Data Analytics Web App in 3 Steps

What Does ChatGPT Say About Machine Learning Trend and How Can We Prepare For It?

An Interactive Guide to Hypothesis Testing in Python

Updated: Jun 12, 2022

upgrade and grab the cheatsheet from our infographics gallery

What is hypothesis testing.

Hypothesis testing is an essential part in inferential statistics where we use observed data in a sample to draw conclusions about unobserved data - often the population.

Implication of hypothesis testing:

clinical research: widely used in psychology, biology and healthcare research to examine the effectiveness of clinical trials

A/B testing: can be applied in business context to improve conversions through testing different versions of campaign incentives, website designs ...

feature selection in machine learning: filter-based feature selection methods use different statistical tests to determine the feature importance

college or university: well, if you major in statistics or data science, it is likely to appear in your exams

For a brief video walkthrough along with the blog, check out my YouTube channel.

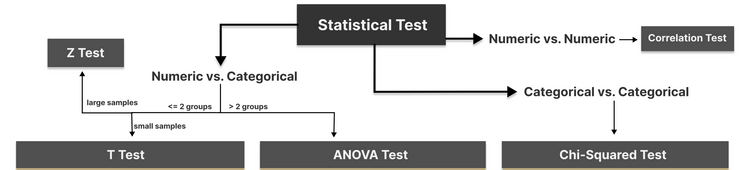
4 Steps in Hypothesis testing

Step 1. define null and alternative hypothesis.

Null hypothesis (H0) can be stated differently depends on the statistical tests, but generalize to the claim that no difference, no relationship or no dependency exists between two or more variables.

Alternative hypothesis (H1) is contradictory to the null hypothesis and it claims that relationships exist. It is the hypothesis that we would like to prove right. However, a more conservational approach is favored in statistics where we always assume null hypothesis is true and try to find evidence to reject the null hypothesis.

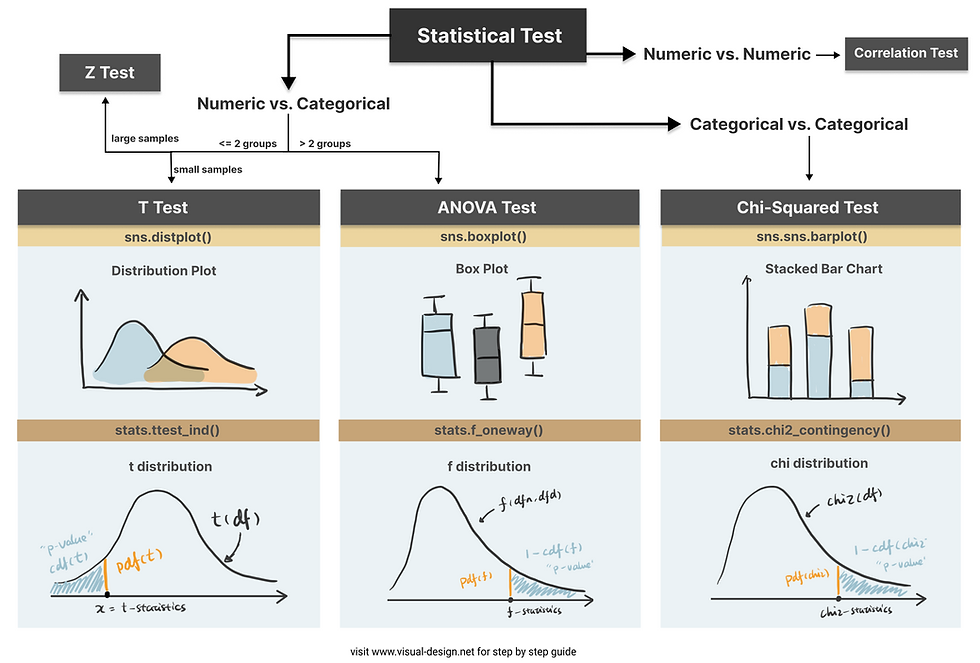
Step 2. Choose the appropriate test

Common Types of Statistical Testing including t-tests, z-tests, anova test and chi-square test

T-test: compare two groups/categories of numeric variables with small sample size

Z-test: compare two groups/categories of numeric variables with large sample size

ANOVA test: compare the difference between two or more groups/categories of numeric variables

Chi-Squared test: examine the relationship between two categorical variables

Correlation test: examine the relationship between two numeric variables

Step 3. Calculate the p-value

How p value is calculated primarily depends on the statistical testing selected. Firstly, based on the mean and standard deviation of the observed sample data, we are able to derive the test statistics value (e.g. t-statistics, f-statistics). Then calculate the probability of getting this test statistics given the distribution of the null hypothesis, we will find out the p-value. We will use some examples to demonstrate this in more detail.

Step 4. Determine the statistical significance

p value is then compared against the significance level (also noted as alpha value) to determine whether there is sufficient evidence to reject the null hypothesis. The significance level is a predetermined probability threshold - commonly 0.05. If p value is larger than the threshold, it means that the value is likely to occur in the distribution when the null hypothesis is true. On the other hand, if lower than significance level, it means it is very unlikely to occur in the null hypothesis distribution - hence reject the null hypothesis.

Hypothesis Testing with Examples

Kaggle dataset “ Customer Personality Analysis” is used in this case study to demonstrate different types of statistical test. T-test, ANOVA and Chi-Square test are sensitive to large sample size, and almost certainly will generate very small p-value when sample size is large . Therefore, I took a random sample (size of 100) from the original data:

T-test is used when we want to test the relationship between a numeric variable and a categorical variable.There are three main types of t-test.

one sample t-test: test the mean of one group against a constant value

two sample t-test: test the difference of means between two groups

paired sample t-test: test the difference of means between two measurements of the same subject

For example, if I would like to test whether “Recency” (the number of days since customer’s last purchase - numeric value) contributes to the prediction of “Response” (whether the customer accepted the offer in the last campaign - categorical value), I can use a two sample t-test.

The first sample would be the “Recency” of customers who accepted the offer:

The second sample would be the “Recency” of customers who rejected the offer:

To compare the “Recency” of these two groups intuitively, we can use histogram (or distplot) to show the distributions.

It appears that positive response have lower Recency compared to negative response. To quantify the difference and make it more scientific, let’s follow the steps in hypothesis testing and carry out a t-test.

Step1. define null and alternative hypothesis

null: there is no difference in Recency between the customers who accepted the offer in the last campaign and who did not accept the offer

alternative: customers who accepted the offer has lower Recency compared to customers who did not accept the offer

Step 2. choose the appropriate test

To test the difference between two independent samples, two-sample t-test is the most appropriate statistical test which follows student t-distribution. The shape of student-t distribution is determined by the degree of freedom, calculated as the sum of two sample size minus 2.

In python, simply import the library scipy.stats and create the t-distribution as below.

Step 3. calculate the p-value

There are some handy functions in Python calculate the probability in a distribution. For any x covered in the range of the distribution, pdf(x) is the probability density function of x — which can be represented as the orange line below, and cdf(x) is the cumulative density function of x — which can be seen as the cumulative area. In this example, we are testing the alternative hypothesis that — Recency of positive response minus the Recency of negative response is less than 0. Therefore we should use a one-tail test and compare the t-statistics we get against the lowest value in this distribution — therefore p-value can be calculated as cdf(t_statistics) in this case.

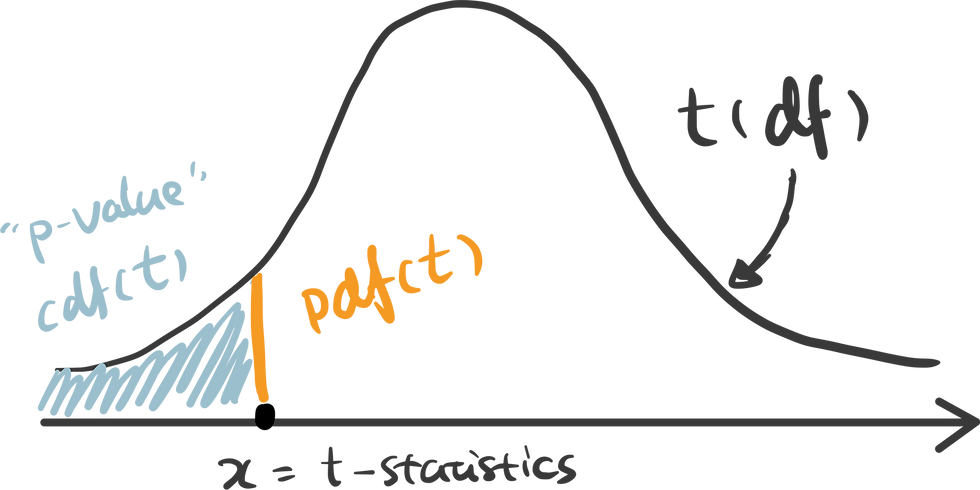
ttest_ind() is a handy function for independent t-test in python that has done all of these for us automatically. Pass two samples rececency_P and recency_N as the parameters, and we get the t-statistics and p-value.

Here I use plotly to visualize the p-value in t-distribution. Hover over the line and see how point probability and p-value changes as the x shifts. The area with filled color highlights the p-value we get for this specific test.

Check out the code in our Code Snippet section, if you want to build this yourself.

An interactive visualization of t-distribution with t-statistics vs. significance level.

Step 4. determine the statistical significance

The commonly used significance level threshold is 0.05. Since p-value here (0.024) is smaller than 0.05, we can say that it is statistically significant based on the collected sample. A lower Recency of customer who accepted the offer is likely not occur by chance. This indicates the feature “Response” may be a strong predictor of the target variable “Recency”. And if we would perform feature selection for a model predicting the "Recency" value, "Response" is likely to have high importance.

Now that we know t-test is used to compare the mean of one or two sample groups. What if we want to test more than two samples? Use ANOVA test.

ANOVA examines the difference among groups by calculating the ratio of variance across different groups vs variance within a group . Larger ratio indicates that the difference across groups is a result of the group difference rather than just random chance.

As an example, I use the feature “Kidhome” for the prediction of “NumWebPurchases”. There are three values of “Kidhome” - 0, 1, 2 which naturally forms three groups.

Firstly, visualize the data. I found box plot to be the most aligned visual representation of ANOVA test.

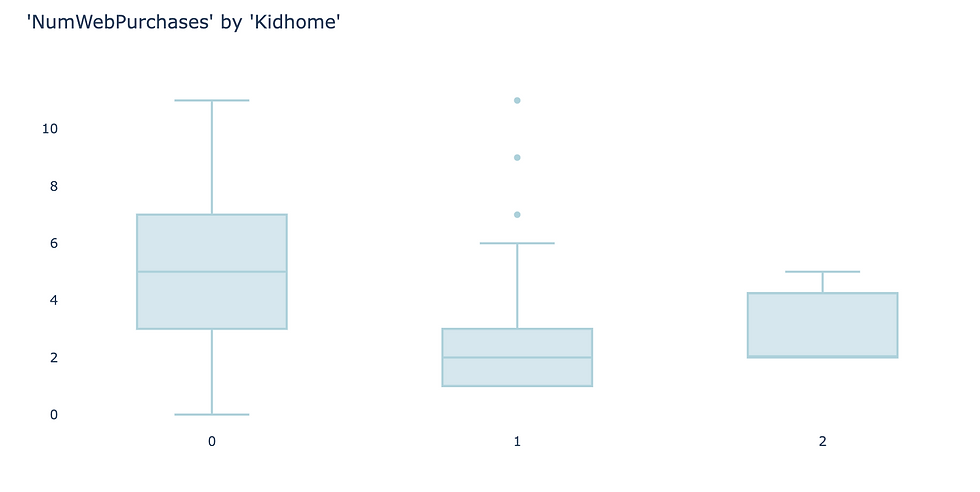
It appears there are distinct differences among three groups. So let’s carry out ANOVA test to prove if that’s the case.

1. define hypothesis:

null hypothesis: there is no difference among three groups

alternative hypothesis: there is difference between at least two groups

2. choose the appropriate test: ANOVA test for examining the relationships of numeric values against a categorical value with more than two groups. Similar to t-test, the null hypothesis of ANOVA test also follows a distribution defined by degrees of freedom. The degrees of freedom in ANOVA is determined by number of total samples (n) and the number of groups (k).

dfn = n - 1

dfd = n - k

3. calculate the p-value: To calculate the p-value of the f-statistics, we use the right tail cumulative area of the f-distribution, which is 1 - rv.cdf(x).

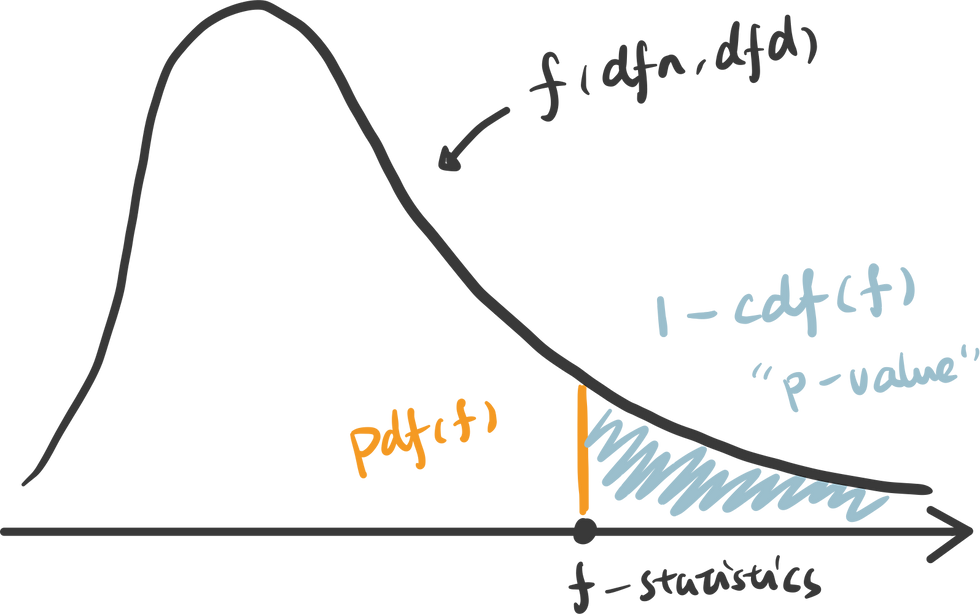
To easily get the f-statistics and p-value using Python, we can use the function stats.f_oneway() which returns p-value: 0.00040.

An interactive visualization of f-distribution with f-statistics vs. significance level. (Check out the code in our Code Snippet section, if you want to build this yourself. )

4. determine the statistical significance : Compare the p-value against the significance level 0.05, we can infer that there is strong evidence against the null hypothesis and very likely that there is difference in “NumWebPurchases” between at least two groups.

Chi-Squared Test

Chi-Squared test is for testing the relationship between two categorical variables. The underlying principle is that if two categorical variables are independent, then one categorical variable should have similar composition when the other categorical variable change. Let’s look at the example of whether “Education” and “Response” are independent.

First, use stacked bar chart and contingency table to summary the count of each category.

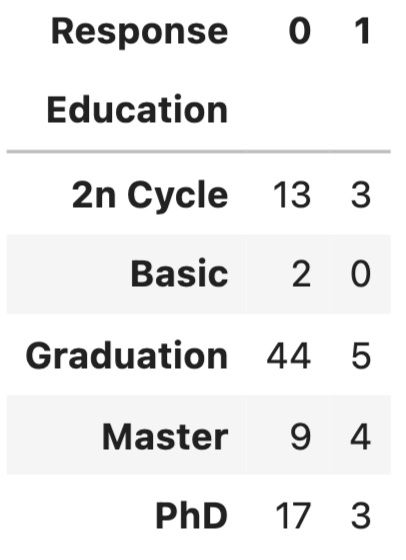
If these two variables are completely independent to each other (null hypothesis is true), then the proportion of positive Response and negative Response should be the same across all Education groups. It seems like composition are slightly different, but is it significant enough to say there is dependency - let’s run a Chi-Squared test.

null hypothesis: “Education” and “Response” are independent to each other.

alternative hypothesis: “Education” and “Response” are dependent to each other.

2. choose the appropriate test: Chi-Squared test is chosen and you probably found a pattern here, that Chi-distribution is also determined by the degree of freedom which is (row - 1) x (column - 1).

3. calculate the p-value: p value is calculated as the right tail cumulative area: 1 - rv.cdf(x).

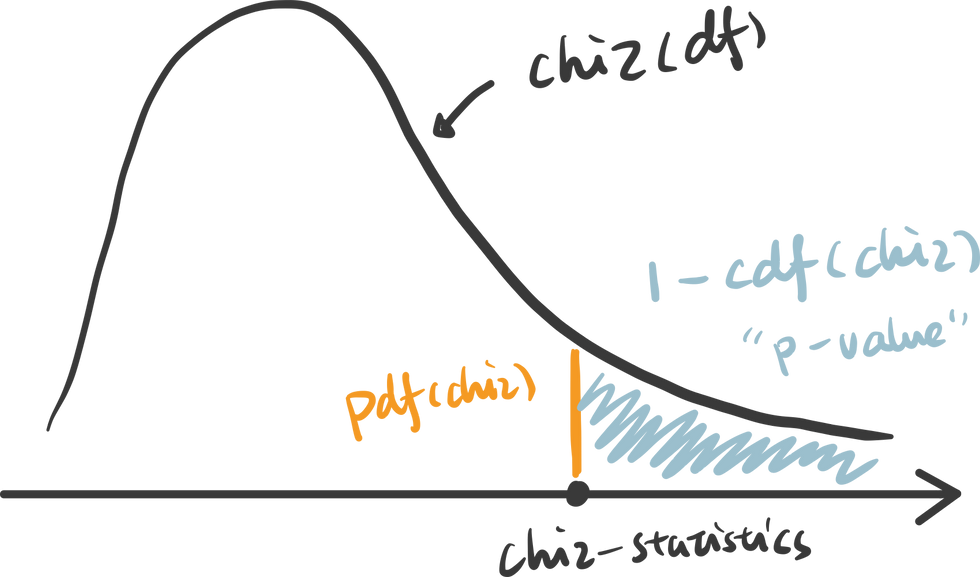
Python also provides a useful function to get the chi statistics and p-value given the contingency table.

An interactive visualization of chi-distribution with chi-statistics vs. significance level. (Check out the code in our Code Snippet section, if you want to build this yourself. )

4. determine the statistical significanc e: the p-value here is 0.41, suggesting that it is not statistical significant. Therefore, we cannot reject the null hypothesis that these two categorical variables are independent. This further indicates that “Education” may not be a strong predictor of “Response”.

Thanks for reaching so far, we have covered a lot of contents in this article but still have two important hypothesis tests that are worth discussing separately in upcoming posts.

z-test: test the difference between two categories of numeric variables - when sample size is LARGE

correlation: test the relationship between two numeric variables

Hope you found this article helpful. If you’d like to support my work and see more articles like this, treat me a coffee ☕️ by signing up Premium Membership with $10 one-off purchase.

Take home message.

In this article, we interactively explore and visualize the difference between three common statistical tests: t-test, ANOVA test and Chi-Squared test. We also use examples to walk through essential steps in hypothesis testing:

1. define the null and alternative hypothesis

2. choose the appropriate test

3. calculate the p-value

4. determine the statistical significance

Data Science

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

Notifications You must be signed in to change notification settings

This GitHub repository contains a Jupyter notebook dedicated to hypothesis testing in Python, offering a thorough introduction to various statistical tests and concepts.

Geoffrey-lab/-Hypothesis-Testing-with-Python-Comprehensive-Notebook

Folders and files, repository files navigation, -hypothesis-testing-with-python-comprehensive-notebook, hypothesis testing with python: comprehensive notebook.

This GitHub repository contains a Jupyter notebook dedicated to hypothesis testing in Python, offering a thorough introduction to various statistical tests and concepts. This resource is designed for data scientists, statisticians, and anyone interested in understanding the fundamental principles of hypothesis testing through practical examples and visualizations.

Repository Contents

Notebook overview.

The notebook is divided into several sections, each focusing on different aspects of hypothesis testing:

Introduction to Hypothesis Testing

Overview of hypothesis testing
Importance and applications in data science

Probability and Distribution Plotting

Calculating probabilities using the normal distribution
Plotting probability density functions (PDF)
Example: Probability of a random data scientist's height being 1.5 meters

One-Sided vs. Two-Sided Hypothesis Tests

Explanation of one-sided and two-sided tests
Visual representation of hypothesis bounds
Example: Testing significance points with standard normal distribution

Type I and Type II Errors

Understanding false positives (Type I errors) and false negatives (Type II errors)

Testing Equality of Means with Known Population Variance

Comparing two sample means
Calculating the Z-statistic
Example: Comparing sample means with known variances

t-Distribution and Sample Variance

Introduction to the t-distribution
Calculating sample variance and degrees of freedom
Example: Hypothesis testing with the t-distribution

Equality of Means with Unknown Population Variance

Using the t-distribution for comparing means with unknown variances
Pooled variance estimation
Example: Testing equality of means with unknown variances

F-Distribution for Testing Equality of Variances

Introduction to the F-distribution
Testing for equality of variances
Example: Visualizing the F-distribution and performing variance tests

Chi-Squared Distribution for Goodness of Fit and Categorical Data

Applying the chi-squared distribution for goodness of fit tests
Example: Factory dingbat rejection rates
Example: Testing independence in a contingency table (left-handedness and smoking)

Key Features

Comprehensive Examples : Each section includes detailed examples with step-by-step explanations and visualizations.
Visualizations : The notebook uses Matplotlib to create clear and informative plots for various distributions and test results.
Code Snippets : Practical code snippets demonstrate how to perform different hypothesis tests using SciPy and NumPy.

Requirements

Jupyter Notebook
Clone the repository: git clone https://github.com/your-username/hypothesis-testing-notebook.git
Navigate to the repository directory: cd hypothesis-testing-notebook
Install the required packages: pip install numpy scipy matplotlib pandas
Launch Jupyter Notebook: jupyter notebook
Open the Hypothesis_Testing_Notebook.ipynb file to start exploring.
Jupyter Notebook 100.0%

Pytest with Eric

How to Use Hypothesis and Pytest for Robust Property-Based Testing in Python

There will always be cases you didn’t consider, making this an ongoing maintenance job. Unit testing solves only some of these issues.

Example-Based Testing vs Property-Based Testing

Project set up, getting started, prerequisites, simple example, source code, simple example — unit tests, example-based testing, running the unit test, property-based testing, complex example, source code, complex example — unit tests, discover bugs with hypothesis, define your own hypothesis strategies, model-based testing in hypothesis, additional reading.